Movimento Uniformemente Variado
1. Durante uma corrida de
carros, um dos competidores consegue atingir 100km/h desde a largada em
5s. Qual a aceleração média por ele descrita?
2. Um móvel, partindo do
repouso com uma aceleração constante igual 1m/s² se desloca durante 5
minutos. Ao final deste tempo, qual é a velocidade por ele adquirida?
3. Um automóvel encontra-se parado diante de um semáforo. Logo quando o sinal abre, ele arranca com aceleração 5m/s², enquanto isso, um caminhão passa por ele com velocidade constante igual a 10m/s.
(a) Depois de quanto tempo o carro alcança o caminhão?
(b) Qual a distância percorrida até o encontro.
Escreve-se as equações do muv para o carro e do mu para o caminhão:
Carro:
Caminhão:
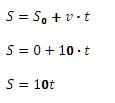
Quando os dois se encontram, suas posições são iguais, então:
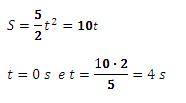
(b) Sabendo o momento do encontro, só é necessário aplicá-lo em uma das duas funções (do caminhão ou do carro).
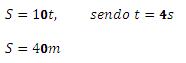
Logo o carro encontra o caminhão 4 segundos após a sinaleira abrir, a uma distância de 40 m.
Como a aceleração utilizada para frear a moto se opõe ao movimento, tem valor negativo, então:
A motocicleta não irá parar antes de atingir a pessoa.
5. Um corredor chega a linha de chegada em uma corrida com velocidade igual a 18m/s. Após a chegada ele anda mais 6 metros até parar completamente. Qual o valor de sua aceleração?
Movimento Vertical
1. Uma pedra é abandonada de um penhasco de 100m de altura. Com que velocidade ela chega ao solo? Quanto tempo demora para chegar?
2. Em uma brincadeira chamada
"Stop" o jogador deve lançar a bola verticalmente para cima e gritar o
nome de alguma pessoa que esteja na brincadeira. Quando a bola retornar
ao chão, o jogador chamado deve segurar a bola e gritar: "Stop", e todos
os outros devem parar, assim a pessoa chamada deve "caçar" os outros
jogadores. Quando uma das crianças lança a bola para cima, esta chega a
uma altura de 15 metros. E retorna ao chão em 6 segundos. Qual a
velocidade inicial do lançamento?
Para realizar este cálculo deve-se dividir o
movimento em subida e descida, mas sabemos que o tempo gasto para a
bola retornar é o dobro do tempo que ele gasta para subir ou descer.
Então:
- Subida (t=3s)
3. Durante a gravação de um
filme, um dublê deve cair de um penhasco de 30m de altura e cair sobre
um colchão. Quando ele chega ao colchão, este sofre uma deformação de
1m. Qual é a desaceleração que o dublê sofre até parar quando chega
colchão?
A desaceleração sofrida pelo dublê se dará
quando a velocidade inicial for a velocidade de chegada ao solo na queda
vertical, a velocidade final for zero, e a distância do deslocamento
for 1m de deformação do colchão. Então o primeiro passo para chegar a
resolução é descobrir a velocidade de chegada ao solo:
Como no exercício não é dado o tempo, a
maneira mais rápida de se calcular a velocidade é através da Equação de
Torricelli para o movimento vertical, com aceleração da gravidade
positiva, já que o movimento é no mesmo sentido da gravidade.
O segundo passo é calcular o movimento uniformemente variado para a desaceleração da queda. Com velocidade inicial igual a 24,5m/s.
4. Um fazendeiro precisa saber
a profundidade de um poço em suas terras. Então, ele abandona uma pedra
na boca do poço e cronometra o tempo que leva para ouvir o som da pedra
no fundo. Ele observa que o tempo cronometrado é 5 segundos. Qual a
altura do poço?
Podemos dividir o movimento em movimento da pedra e o deslocamento do som.
- Movimento da Pedra:
- Deslocamento do som:
Sabendo que a altura do poço é a mesma para as duas funções e que
mas
Sabendo que
Tendo os tempos de cada movimento, podemos calcular a altura utilizando qualquer uma das duas funções:

Nenhum comentário:
Postar um comentário