- POLINOMIOS DE CHEBYSHEV= Em matemática, os Polinómios de Chebyshev (pt-PT) ou Polinômios de Tchebychev (pt-BR), receberam esse nome após matemático Pafnuty Chebyshev[1] defini-los como uma sequência de polinômios ortogonais, relacionados com a fórmula de Moivre e facilmente obtíveis de forma recursiva. Costuma-se denotar os polinômios de Tchebychev de primeira ordem por Tn o os polinômios de Tchebychev de segunda ordem por Un. O uso da letra T para os polinômios de primeira ordem foi dado devido a uma das trasliterações de Tchebychev, que admitem também Chebyshev, Tchebyshef e Tschebyscheff.
Os polinômios de Tchebychev Tn ou Un são polinômios de grau n e a sequência dos polinômios de todos os graus formam uma sequência polinomial.
Os polinômios de Tchebyshev são importantes na teoria da aproximação porque as raízes dos polinômios de primeira ordem podem ser utilizados na interpolação polinomial. O resultado da interpolação minimiza o problema do fenômeno de Runge e fornece a melhor aproximação de uma função contínua que obedece à norma do supremo. Essa aproximação conduz diretamente ao método da quadratura de Clenshaw–Curtis.
No estudo de equações diferenciais os polinômios de Tchebychev surgem como soluções das equações de Chebyshev
- POLINOMIOS DE HERMITE= Os polinômios de Hermite são um exemplo de polinômios ortogonais cujo principal campo de aplicação encontra-se na mecânica quântica, especialmente no estudo do oscilador harmônico unidimensional. São nomeados assim em homenagem a Charles Hermite.
Os polinômios de Hermite ("polinômios de Hermite probabilísticos") são definidos por:
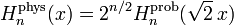 .
.

- POLINOMIO DE LEGENDRE= Na matemática, funções de Legendre são soluções da equação diferencial de Legendre:
A equação diferencial de Legendre pode ser resolvida utilizando o método de série de potências usual. A equação possui um ponto singular regular em x= ± 1 então, em geral, uma solução com séries em relação a origem somente convergirá se |x| < 1. Quando n é um inteiro, a solução Pn(x) que é regular em x=1 é também regular em x=-1, e a série para esta solução é finita (i.e. é um polinômio).
Esta solução para n = 0, 1, 2,... (com a normalização Pn(1)=1) forma uma seqüência polinomial de polinômios ortogonais chamados polinômios de Legendre. Cada polinômio de Legendre Pn(x) é um polinômio de n-ésimo grau. Isto pode ser expresso utilizando a fórmula de Rodrigues:
- POLINOMIO DE BERNSTEIN= Em matemática, um polinômio de Bernstein é um polinômio da forma:
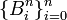 forma uma base para os polinômios de grau até n. Isto é, se P(x) é um polinômio de grau menor ou igual a n, então pode ser escrito na forma:
forma uma base para os polinômios de grau até n. Isto é, se P(x) é um polinômio de grau menor ou igual a n, então pode ser escrito na forma:

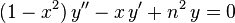

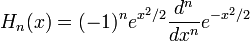

![{d \over dx} \left[(1-x^2) {d \over dx} P_n(x) \right] + n(n+1)P_n(x) = 0.](http://upload.wikimedia.org/math/5/2/b/52bff80109b66b45a6fb0ea62522a03f.png)
![P_n(x) = {1 \over 2^n n!} {d^n \over dx^n } \left[(x^2 -1)^n \right].](http://upload.wikimedia.org/math/7/0/a/70a1790c4fb6b05d9ccea331b0dabe51.png)
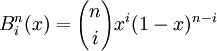
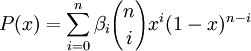
Nenhum comentário:
Postar um comentário