Questões - Indução Magnética

1. Uma espira retangular, com 15cm de largura, por 20cm de comprimento encontra-se imersa em um campo de indução magnética uniforme e constante, de módulo 10T. As linhas de indução formam um ângulo de 30° com o plano da espira, conforme mostra a figura:

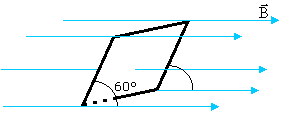
Qual é o valor do fluxo de indução magnética que passa pela espira?

Para resolver este problema, devemos lembrar da expressão que calcula o fluxo de indução:

Mas é importante lembrar que o ângulo θ é o que se forma entre a direção do campo magnético e a reta normal à espira. Para analisar melhor este ângulo, podemos redesenhar a figura em perfil:

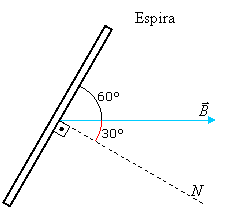
Conculindo que o ângulo θ é igual a 30°, e que a área interna à espira é 0,15m x 0,2m=0,03m², podemos calcular o fluxo de indução:

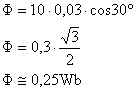
2. Um campo magnético atua perpendicularmente sobre uma espira circular de raio 10cm, gerando um fluxo de indução magnética de 1Wb. Qual a intensidade do campo magnético?

Sendo a área da espira:

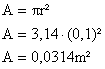
Então a intensidade do campo magnético pode ser calculada por:

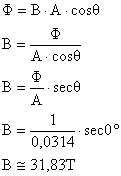
Saiba mais... No equacionamento acima foi usado uma convenção trigonométrica de secante (secθ = 1/cosθ). Caso o estudante não domine completamente esta função trigonométrica, usar o cosseno no denominador não trará maiores problemas, a não ser quando θ=90° e seus equivalentes (90°+180°k), que ocasionará uma indeterminação no cálculo.

3. Uma espira quadrada de lado R= 2cm é imersa em um campo magnético uniforme de intensidade 2T. Qual é o fluxo de indução nessa espira em cada um dos seguintes casos:

a) o plano da espira é paralelo às linhas de indução;

Neste caso, a reta normal à espira têm ângulo de 90°, e cos90° =0, portanto, ao aplicarmos este valor na equação, ele a anulará, fazendo com que o fluxo de indução seja nulo, ou seja

Φ = 0

b) o plano da espira é perpendicular às linhas de indução;

Neste caso, a reta normal à espira não formará ângulo com as linhas de indução (θ=0), e cos0° =1, portanto, ao aplicarmos este valor na equação faremos com que seu valor seja máximo, já que todos os outros valores do cosseno são menores que 1. Portanto:

Sendo A=0,2²=0,04m² :

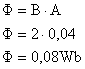
c) o reta normal ao plano forma um ângulo de 60° com as linhas de indução.

Como há ângulo entre 0° e 90° entre a reta normal e as linhas de indução, usamos a equação generalizada para resolver: